genetic-correlations-in-ldsc
Genetic correlation in LD score regression
This lecture:
the LDSC genetic correlation estimator
Making sure the LD score you use, are appropriate for the cohort/GWAS you have,
The Practical!
Get the data for the practical
Lets start grabbing the data, its a bit more data then some of the other practicals.
Code is in the forum (“ISG Workshop logisitcs”), and in the shared files
Genetic correlation in LD score regression
Univariate LDSC:
\[Z_{j}^2 = \frac{ N * h^2_{snp} }{M}*l_j + 1 + Na\]
Bivariate LDSC:
\[Z_{1j} *Z_{2j} = \frac{ \sqrt{N_{1} N_{2}} * cov_g }{M}*l_j + \frac{cor_p * N_s}{\sqrt{N_{1} N_{2}}} + \sqrt{N_{1} N_{2}}*cor(a_1,a_2)\]
Bulik-Sullivan, B., Finucane, H. K., Anttila, V., Gusev, A., Day, F. R., Loh, P. R., … & Neale, B. M. (2015). An atlas of genetic correlations across human diseases and traits. Nature genetics, 47(11), 1236-1241.
LDSC as a regression
Bivariate LDSC:
\[Z_{1j} *Z_{2j} = \frac{ \sqrt{N_{1} N_{2}} * cov_g }{M}*l_j + \frac{cor_p * N_s}{\sqrt{N_{1} N_{2}}} + \sqrt{N_{1} N_{2}}*cor(a_1,a_2)\]
It’s just a regression:
\[y_j = b*l_j + a\]
Data
GWAS sumstats for traits 1 and 2 for SNP j:
\[Z_{1j} *Z_{2j}\]
Audience Q: “What is this Z?”
The LD score, a per SNP measure of the size of the part of the genome tagged by SNP j:
\[l_i\]
Parameters
\[ b = \frac{\sqrt{N_{1} N_{2}} * cov_g}{M} = slope\]
\[ a = \frac{cor_p * N_s}{\sqrt{N_{1} N_{2}}} + a = intercept\]
Works for GWAS that do not overlap!

BUT!
Its a regression where the “outcome” (GWAS results) and the “predictor” (LD score) come form different sources…
That’s really weird… and it puts a little bit of responsibility on the user to ensure the variables are from a common population…
A look at variation in the LD map
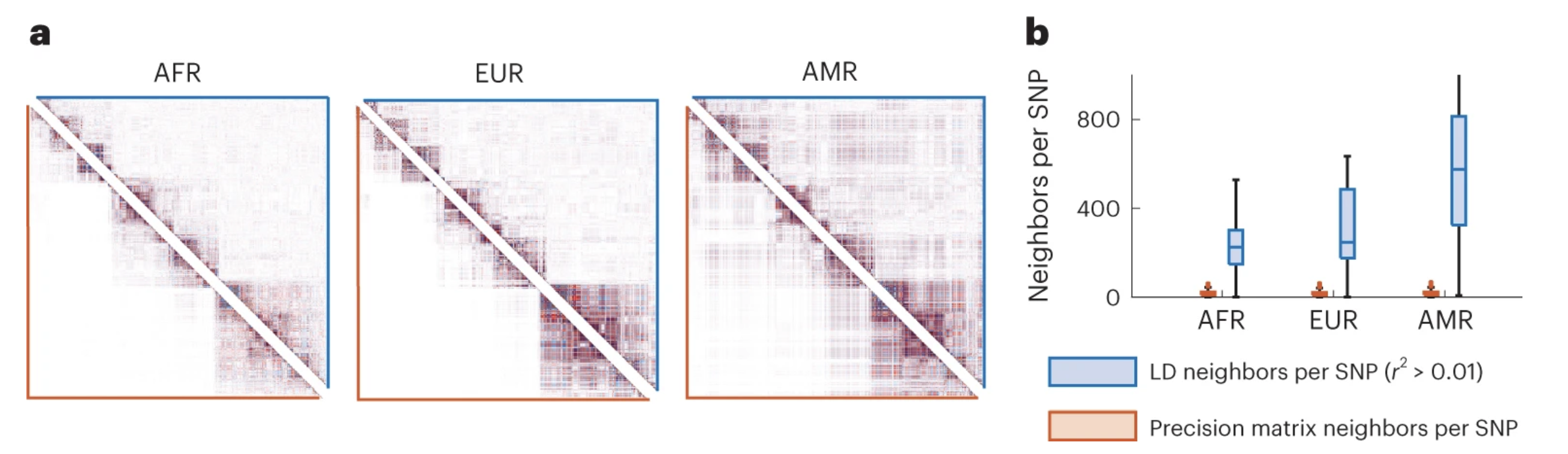
Salehi Nowbandegani, P., Wohns, A. W., Ballard, J. L., Lander, E. S., Bloemendal, A., Neale, B. M., & O’Connor, L. J. (2023). Extremely sparse models of linkage disequilibrium in ancestrally diverse association studies. Nature Genetics, 55(9), 1494-1502.
So we want to match ancestry in the LDscore to the GWAS sample
Use ancestry specific LD scores, for example:
- GNOMAD: https://gnomad.broadinstitute.org/downloads#v2-linkage-disequilibrium
- UKBiobank Pan ancestry: https://pan-dev.ukbb.broadinstitute.org/downloads
What if I still don’t really think their appropriate for my sample?
- Make your won LD scores: https://github.com/bulik/ldsc/wiki/LD-Score-Estimation-Tutorial
- (You need sequencing data!)
Can we use LDSC in admixed samples?
- Many people have multiple ancestries

How can we use cov-LDSC in admixed samples?
Use “covariate adjusted” LD scores in admixed samples.
cov-LDSC software: https://github.com/immunogenomics/cov-ldsc
What if you want to compute the rg between GWASs in different ancestries?
- There is a tool called popcorn that models the differences in LD and AF and rg at the same time
- https://github.com/brielin/Popcorn
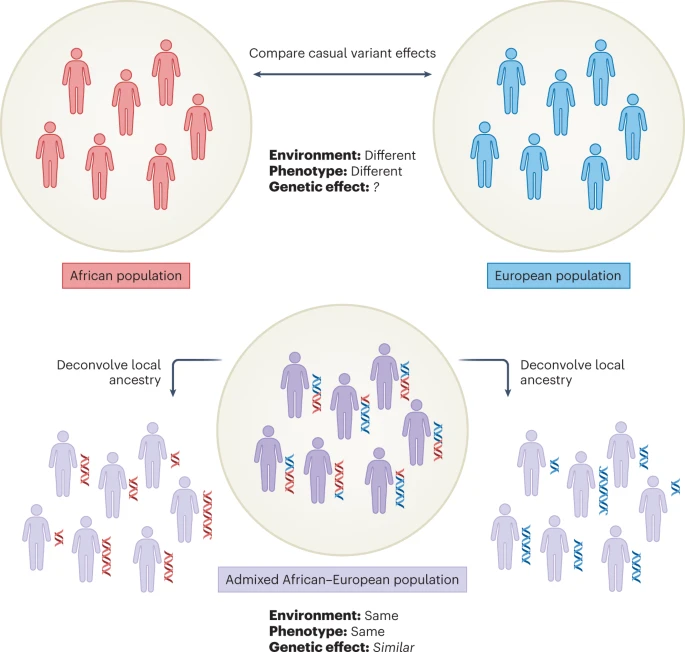
What if you want to compute the rg between GWASs in different ancestries?
BUT it obviously also pulls in all cultural, cohort, measurement differences between your GWASs!
Solutions: compute rg between traits, within an admixed person correlating the genetic effects betwene their two ancestries.
Acessible explanation: https://www.nature.com/articles/s41588-023-01325-x
Original paper: https://www.nature.com/articles/s41588-023-01338-6
Software: https://github.com/KangchengHou/admix-kit
Popcorn vs Admix-kit
Let’s look at the practical for today!
we have GWAS data and LD scores of MDD and BMI for people of European and east-Asian ancestry
What is YOUR estimand? (what do YOU want to know?)
We estimate the rg’s using LDSC (estimator)
We see if we can learn about your estimand using our estimates?