Causes of Covariation

Michel Nivard

Flamingo’s

Causes of covariation

Today will cover ways to model the genetic covariance, and correlation, between two, or more traits.

This hour will cover:

• What co correlation is (and isn’t)
• How to relate what you want to know, to a statistical result

What is a correlation?

• a quantification of the degree to which two variables are linearly related
• correlation implies dependence
• dependence DOES NOT imply correlation

Examples of dependence vs correlation

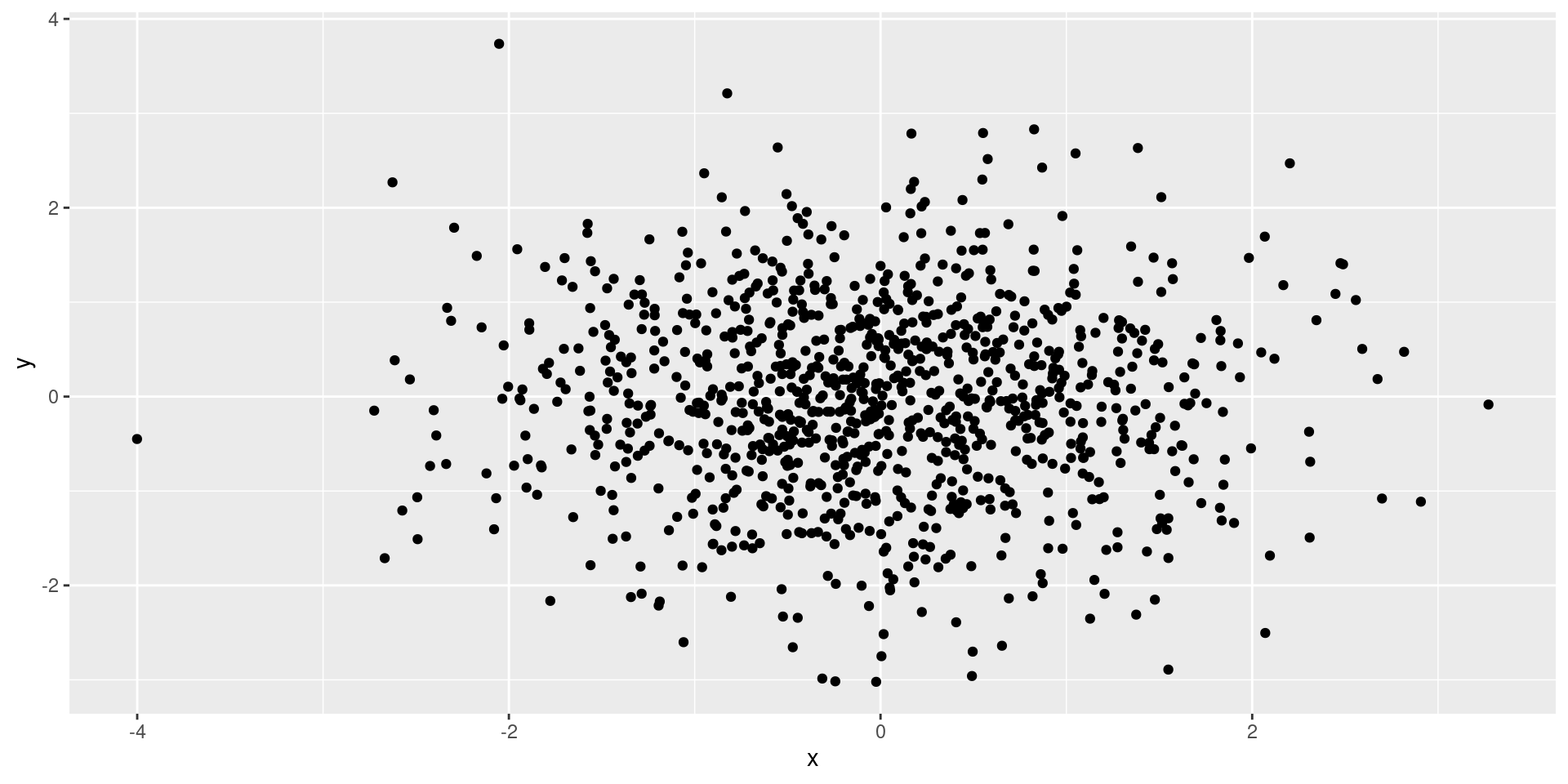
Uncorrelated

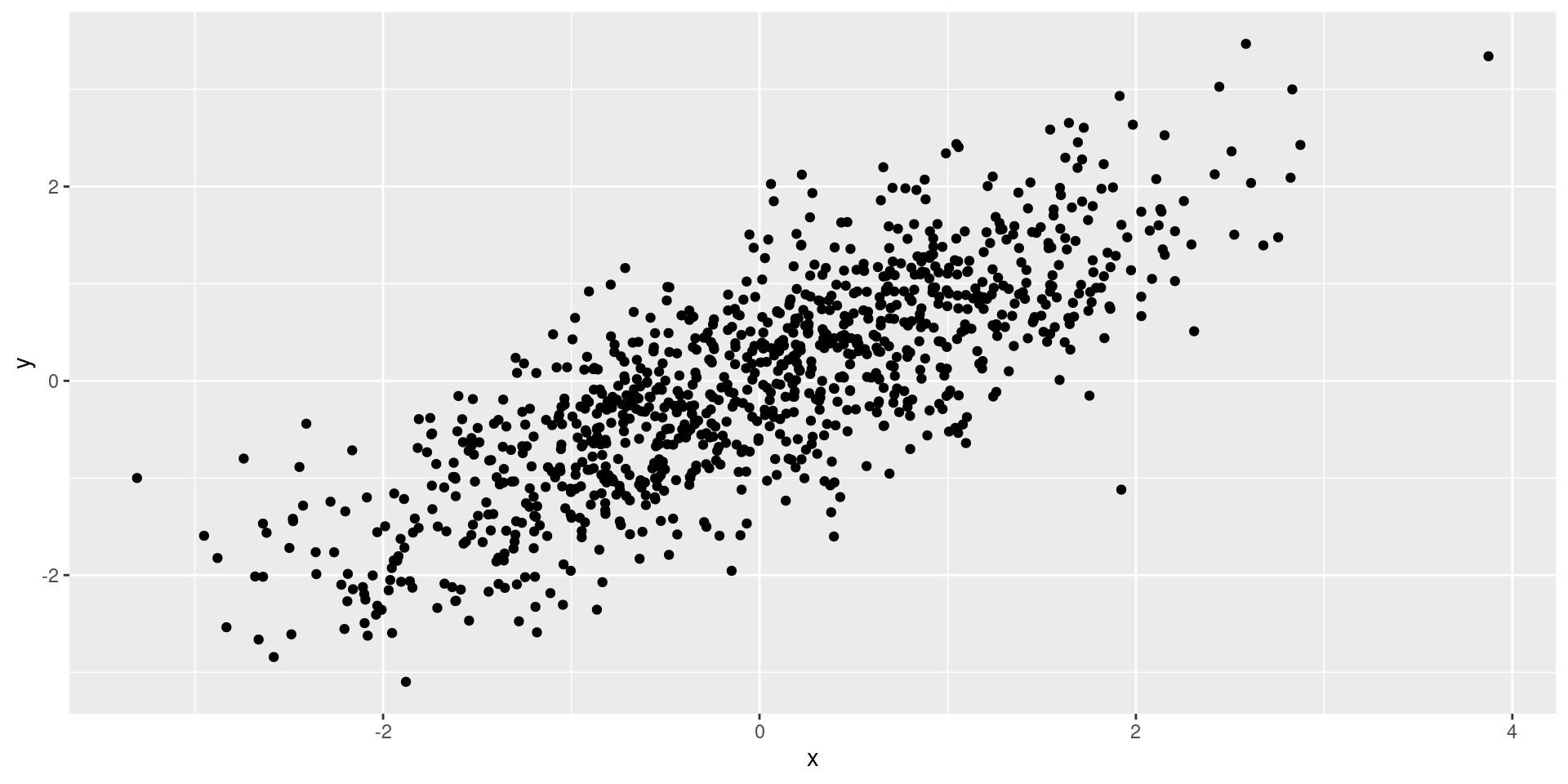
Correlated

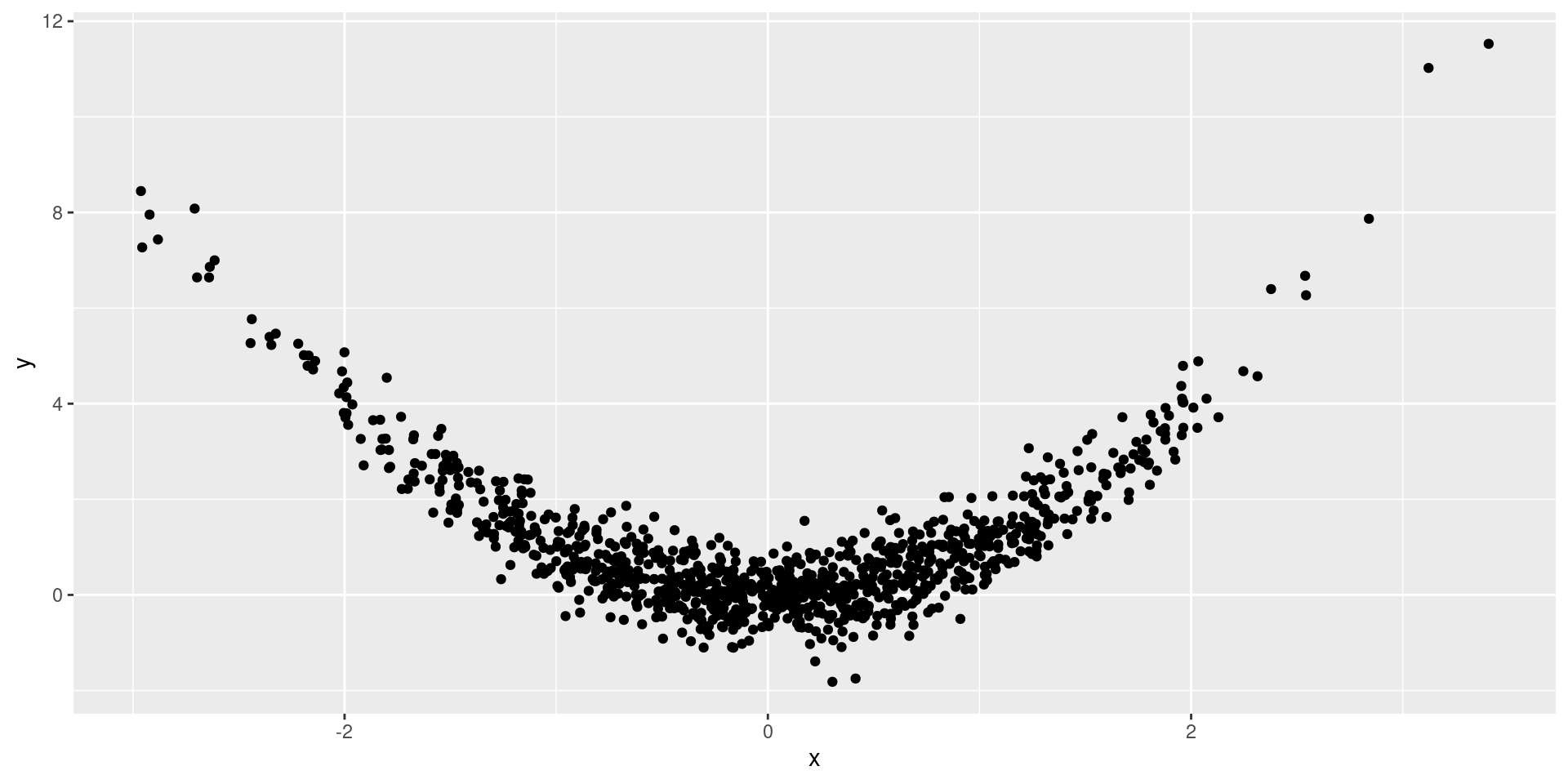
Functionally related, but is it correlated?

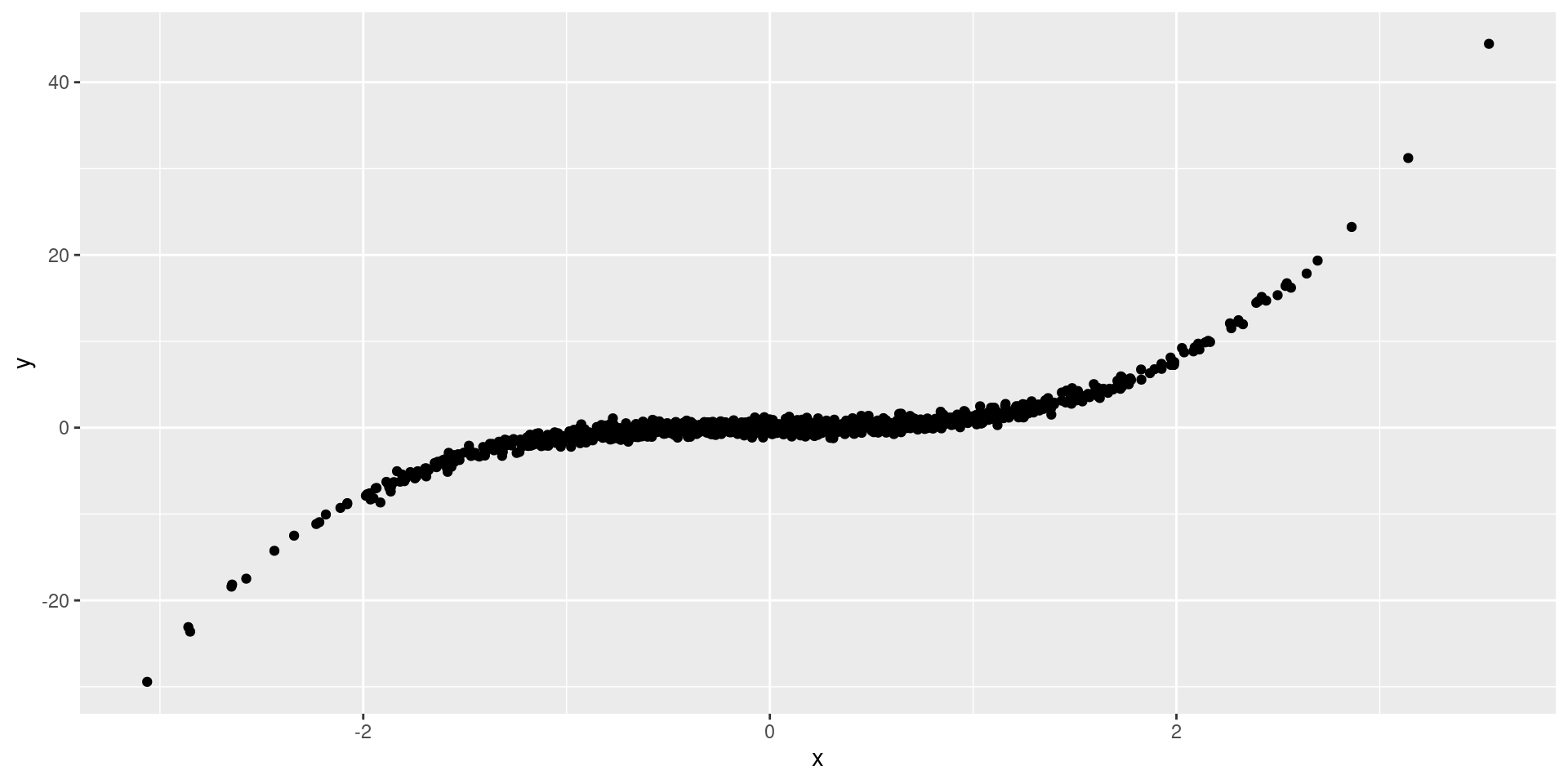
Functionally related, but is it correlated?

Dependent, likely uncorrelated…

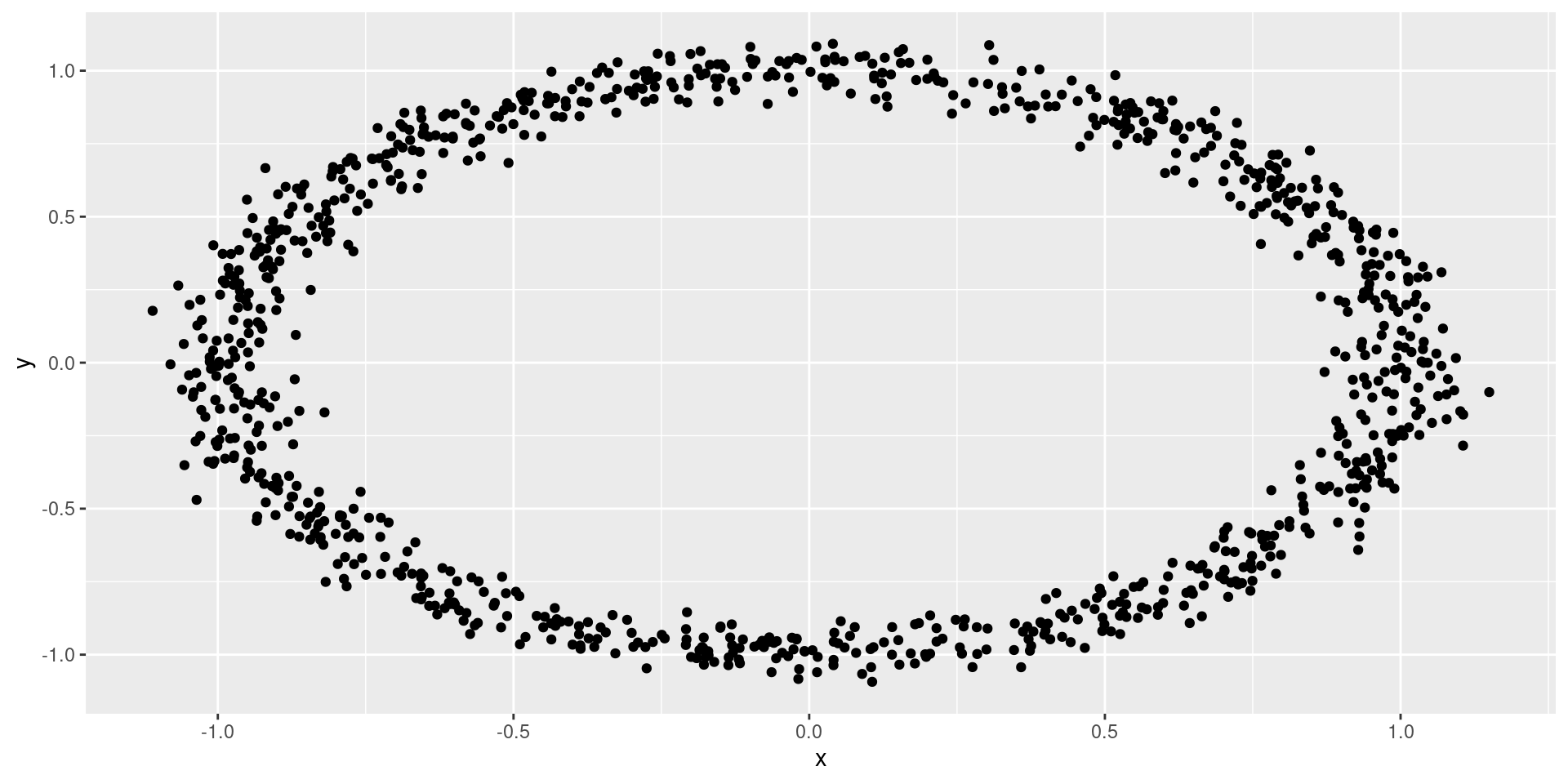
scatterplots go brrr

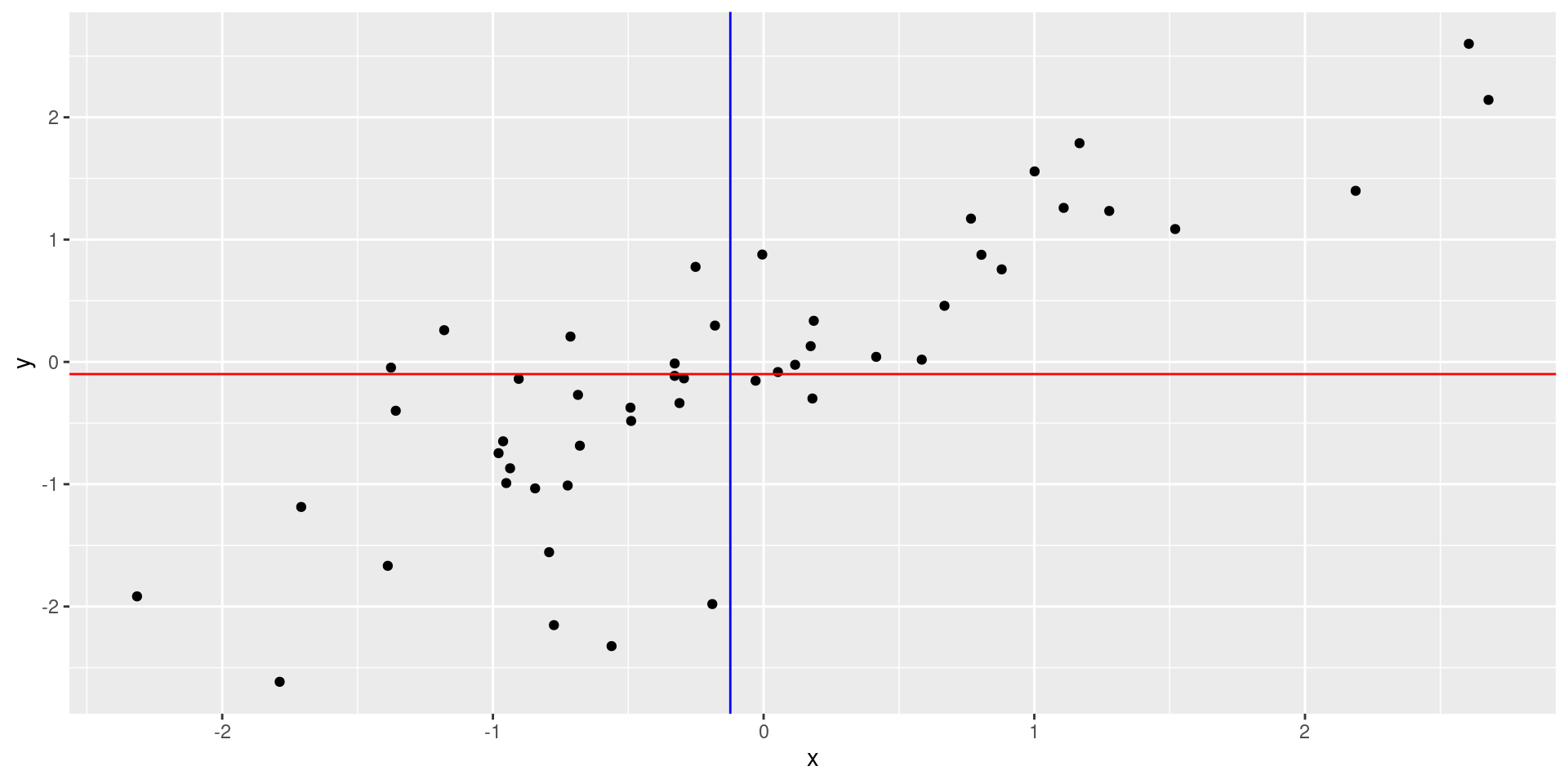
A common estimator of covariance

\[cov_{x,y} = \sum_{i = 1}^{n}{\frac{(x_i-\color{blue}{\bar{x}})*(y_i-\color{red}{\bar{y}})}{N-1}}\]

A common estimator of covariance

\[var_{x} = \sum_{i = 1}^{n}{\frac{(x_i-\color{blue}{\bar{x}})*(x_i-\color{red}{\bar{x}})}{N-1}}\]

\[var_{x} = \sum_{i = 1}^{n}{\frac{(x_i-\color{blue}{\bar{x}})^2}{N-1}}\]

A common estimator of corelations

\[cor_{x,y} = {\frac{cov_{x,y}}{\sqrt{var_x * var_y}}}\]

Two definition of genetic correlation…

\[p1 = a1 + c1 + e1\]

\[p2 = a2 + c2 + e2\] \[r_g = cor(a1,a2)\]

Two definition of genetic correlation…

\[p1_i = \sum_{j = 1}^{m}{(b1_j*snp_j)} +e_i\] \[p2_i = \sum_{j = 1}^{m}{(b2_j*snp_j)} +e_i\]

\[r_g = cor(b_1,b_2)\]

Lets play a game!

correlation game

From research question, to statistical output

• How to relate what you want to know, to a statistical result?

What is it that you want to know?

“are risk for depression and BMI genetically correlated?”

How will you go and find out?

“we will apply LD score regression to two sets of GWAS summary data form two different consortia, that studied BMI and MDD”

What did you find?

“The estimate of the genetic correlation between the PGC MDD, and GIANT BMI GWASs, Using LD score regression is 0.09”

Lets go over this step by step

An estimand is a quantity that is to be estimated in a statistical analysis. The term is used to distinguish the target of inference (estimand) from the method used to obtain an approximation of this target (i.e., the estimator) and the specific value obtained from a given method and dataset (i.e., the estimate).

(genetic) correlation, estimands and estimate

• We almost always want to know about processes that move the estimand
• The diagram below, depends on your estimand!

flowchart LR
  A(common cause) --> D(Estimand correlation)
  B(BMI -> Dep) --> D
  C(Dep -> BMI) --> D
  
  D --> E[estimator]
  E --> H[Estimate correlation]
  F[sampling] --> H[Estimate correlation]
  G[measurement] --> H[Estimate correlation]

correlation, estimands and estimate

• We almost always want to know about processes that move the estimand
• The diagram below, depends on your estimand!

causation, estimands and estimate

• If we change the estimand, or estimator the diagram shifts!
• Estimand: “The causal effect of BMI on Depression”

flowchart LR
  B(BMI -> Dep) --> D(Estimand)
  
  
  A(common cause) --> H[Estimate correlation]
  C(Dep -> BMI) --> H
  D --> E[estimator]
  E --> H
  F[sampling] --> H
  G[measurement] --> H

causation, estimands and estimate

• If we change the estimand, or estimator the diagram shifts!
• Estimand: “The causal effect of BMI on Depression”

Lets look at some specific cases…

flowchart LR
  D(Estimand correlation) --> G[Estimate]
  E[sampling] --> G[Estimate]
  F[measurement] --> G[Estimate]

There are some very specific causes of correlation we need to discuss:

• ascertainment (and colider bias)
• measurement (and measurement error)

Ascertainment & measurement

• The people in your study aren’t always representative of the population (sampling)
• The measurement of your trait is not the same as your trait (measurement)
• These aspects of a study can arise by design, or unintentionally

Ascertainment by design

• Over-sample cases in a schizophrenia GWAS (because its rare)

• Target a study at a specific populations with specific health needs

• You will need to adjust your estimator of \(h^2\)!!

Unintentional ascertainment (usually sampling)

• participants who social economic position is fragile might not have the time to spare for a day long lab study at a location that has poor access via public transport

• Elderly people might only respond to email if their 1. online 2. able too

• level of institutional trust may influence people’s willingness to consent

unintentional ascertainment (sampling)

• Why would I care?

• It will bias all(!!) statistical estimates and inference

• There is a long causal chain between population and sample

unintentional ascertainment (sampling): Collider bias

• if: outcome1 -> ascertainment & outcome2 -> ascertainment

• in the ascertained sample outcome1 and outcome2 will correlate!

Collider bias: dating example

• Why do people feel their more attractive partners where also more toxic?

• Maybe its true? (maybe it effects my estimand)

• Or is it collider bias? (or it effects my estimate)

Collider bias: dating example

Collider bias: dating example

How common is this? Should I care?

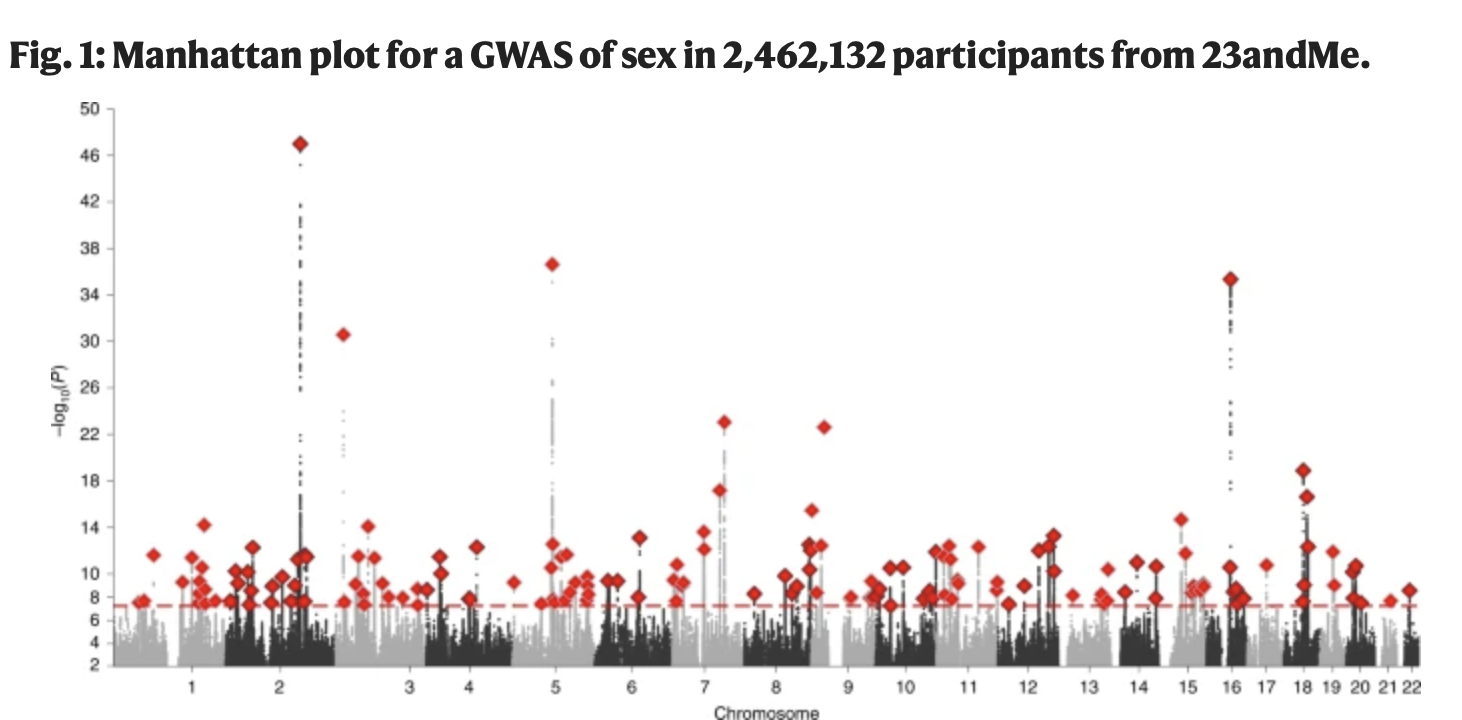
How common is this? Should I care?

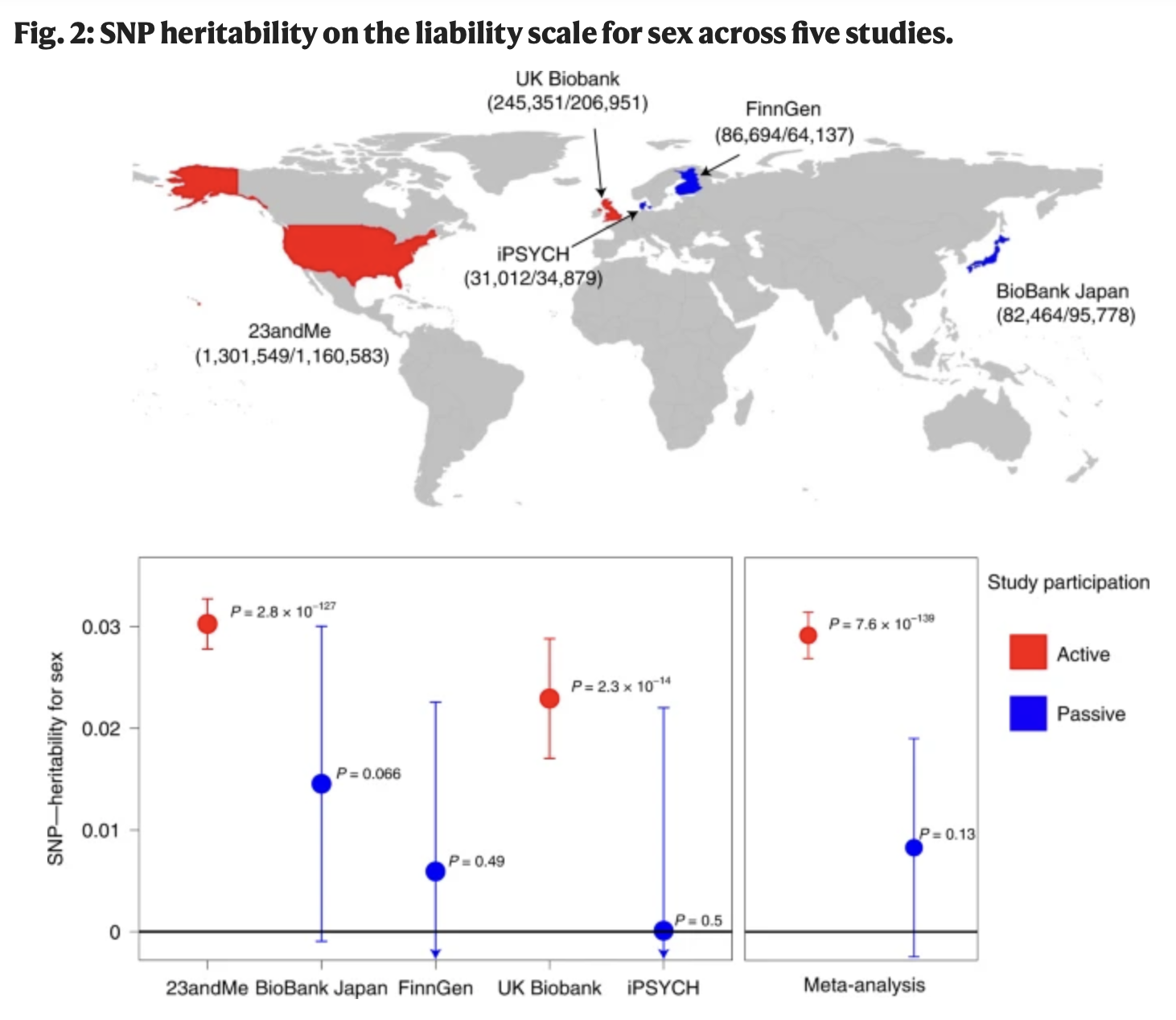
The causes of a (genetic) correlation that we do care about?

• (latent) common cause

• causal relation between two traits

A common cause

flowchart TB
  D(SNP) --> G[astma]
  D(SNP) --> H[stress]

ALSO a common cause

flowchart TB
  D(SNP) --> E[smoking]
  E --> G[astma]
  E --> H[stress]

A causal effect

flowchart LR
  D(SNP) --> E[lung cancer]

ALSO a causal effect

flowchart LR
  C(SNP) --> D[smoking] --> E[lung cancer]

Take home

• You have to consider what you want to know (estimand) carefully
• This will help you understand what your actually estimate means
• When analyzing the relation bertween two or more traits, consider all the causes of covariation!

Glance at the rest of the day:

• Margot will discuss estimating genetic correlation between two traits, using twin/family data.
• Brad will discuss models for the genetic correlations between more than 2 traits in family data
• I will discuss estimators of genetic correlation based on GWAS summary data (LDSC/Genomic SEM)
• Andrew will discuss models for the genetic correlations between more than 2 traits based on GWAS summary data (LDSC/Genomic SEM)

bivariate twin model with Margot

\[p1 = a1 + c1 + e1\]

\[p2 = a2 + c2 + e2\]

\[r_g = cor(a1,a2)\]

bivariate twin model with Margot

\[Vp1_{mz} = Va1 + Vc1 + Ve1\]

\[cov(p1_{mz1},p1_{mz2}) = Va1 + Vc1\]

bivariate twin model with Margot

\[Vp1 = Va1 + Vc1 + Ve1\] \[Vp2 = Va2 + Vc2 + Ve2\] \[cov(p1_{mz1},p2_{mz2}) = Coc(a1,a2) + Cov(c1,c2)\]

Bivariate molecular model with Me

• we can do a ry similar thing with GWAS summary data.

\[p1_i = \sum_{j = 1}^{m}{(b1_j*snp_j)} +e_i\] \[p2_i = \sum_{j = 1}^{m}{(b2_j*snp_j)} +e_i\]

\[r_g = cor(b_1,b_2)\] ## genetic correlations

• The bivariate twin model, and LDSC are complementary estimators of a similar quantity
• Its not an identical quantity(!)

Latent variable models with Brad & Andrew

flowchart TB
  D(latent_variable) --> E[Depression]
  D --> G[Anxiety]
  D --> H[PTSD]

Latent variable models with Brad & Andrew

flowchart TB
  A(A) --> D(latent_variable)
  B(E) --> D(latent_variable)
  D --> E[Depression]
  D --> G[Anxiety]
  D --> H[PTSD]

Or…

flowchart TB
  D(E) --> F[Depression]
  D --> G[Anxiety]
  D --> H[PTSD]
  
  E(A) --> F[Depression]
  E --> G[Anxiety]
  E --> H[PTSD]

Genetics in the context of genetic latent variable modeling

• Brad and Andrew discuss complimentary estimators of genetic latent variable models
• The methods and code might look very different, various concepts are shared